28 June-05 July 2025
Hello, dear readers!
I look forward to celebrating the longest day of the year and the official start of summer, but this year I spent the longest day huddled in the basement. We had a “heat dome” last week with high temperatures and unusually high humidity. Air temperatures were nearly 100 degrees here for several days in a row, with the heat index reaching and exceeding 110. The highest readings I saw for temperature and heat index were 99 and 112, respectively. Not only did the “heat dome” break daily records for high temperatures, but it broke daily records for highest lows.
Alpena, Michigan: Their daily low of 79 degrees Monday topped their previous record of 77 set three other times in 1919, 1927 and 1948.
Eau Claire, Wisconsin: Their daily low of 82 degrees Sunday topped their previous record of 81 set both on June 27, 1991 and July 20, 1932.
We had similar evening lows here. I mention the hot and humid evenings specifically because they are dangerous:
High nighttime temperatures are detrimental to human health, as they prevent the body from recovering from daytime heat. This not only disrupts sleep, which can negatively affect physical and mental health, cognitive function, and life expectancy, but it also increases the risk of illness and mortality.
We are very fortunate that the power stayed on, as I was expecting it would likely fail due to the poor condition of our local grid. So, our air conditioning system continued to run. When it reached 99 degrees, our system wasn’t able to keep the indoor temperature at or below 80. It was more like 82 or 83 by evening, and only came down a few more degrees during the night. The air conditoning system was able to reduce the humidity, but not as much as we’d like. The basement doesn’t have ducts for the air conditioning system, so it doesn’t help the humidity down there — I was running two dehumidifiers, emptying their buckets twice a day, and they were barely keeping up; also, dehumidifiers put out heat.
A few days after the heat wave had passed, the older and smaller of the two dehumidifiers started producing a strong smell of burning insulation, so I had to shut it down. I don’t think I ever mentioned it in my newsletters, but last year we bought a brand new GE dehumidifier, which only worked for a few months before failing with an undocumented error code. No one, including GE, will repair these units. GE tried to convince me that I should accept a voucher for a partial refund of the cost of another GE dehumidifier, which I had to buy first before I could get the voucher. That’s not what the printed warranty offers, so I refused to sign that paperwork and wrote back to them again and again until they finally agreed to ship a new unit at no cost to me. It took months, but a new unit eventually arrived. But the dead one is still downstairs. So now we’ve got two dead dehumidifiers to dispose of. I’ve gone through so many of these stupid things over the years.
Upstairs, the refrigerator was struggling to keep things cool enough. The cream, in the front of the fridge, went bad early. The greens that were too close to the back froze.
On Tuesday I took Grace to a dental appointment. Breathing the air was uncomfortable — it felt like breathing soup! I put two emergency cooling vests from the freezer into their insulated bags and we took them in the car with us, in case we had a breakdown. Fortunately, the air conditioning in the car was working. Grace has always had trouble tolerating high heat. I can manage it a little bit better, but heat and humidity like this will get to anyone who doesn’t have access to cooling.
When the heat dome finally started to move, several of us developed headaches — the air pressure dropped very rapidly. When this happens I literally hear creaking noises inside my inner ears and sinuses. When this happens, I fear we’ll lose power, and maybe have flooding, due to the thunderstorms that usually blow through. Fortunately, the storms that passed over us weren’t very severe.
We’re now having temperatures that are closer to typical late-June temperatures, although on the high side. The humidity is far more bearable. Today, Saturday, three of our kids are at a COVID-safe alternative “prom” — an outdoor dance party — for homeschooled and COVID-cautious kids. My son Joshua, 16, did much of the hard and tedious organizing work to plan this event. I continue to be amazed by his tenacity and hard work and the way he has stuck by the precautionary principle to organize an event that will be safe for everyone. I’m at home watching the rest of the kids, but I did get some pictures before they left, and they took “Cambot” — an iPhone we use only for taking pictures and video — with them. I haven’t processed all those photos yet, but here’s a photo I took of the three kids we took, Veronica, Joshua, and Benjamin:
I’m pleased to report that after more than a year of mostly-steady, sometimes-tedious effort, I have finished the Foundations II online course from Math Academy. A list of topics covered can be found here. There are almost 350 of them. There’s a lesson for each topic, usually with 5 to 10 problems included, and then the material is presented again and again with shorter review assignements, usually with 3 to 5 review problems. The system attempts to give me a quiz roughly once a week, although because the amount of work I did varied from week to week, they weren’t quite weekly. In addition to the quizzes, there were occasional “multistep” assignments, which aren’t timed. Multisteps give you some initial information, for example the definitions of three functions, and then ask you to complete six or seven increasingly difficult problems, most of which build on previous results.
I wrote everything out — topic summaries, lesson problems, review problems, and multi-steps — in a series of notebooks. I didn’t do the quiz problems in the notebooks. The quizzes were timed, so I didn’t want to take the time to write every step out using my best printing. I’d do the quizzes on scrap paper. After each quiz, if there were any problems I got wrong, I wrote those out in my notebooks, with the correct answers. If there was a question I got right, but I found it especially difficult or interesting, and I got them right, I’d write those out, too.
All told, I filled twelve notebooks, and nearly filled the thirteenth.
I don’t have my notebooks or assignments from high school, but I think I may have written out more math notes and problems for this single class than I did for all of the math classes I took in both high school and college.
After over a year of this, I now find that I make algebra and arithmetic errors much less often. I can occasionally skip writing out steps. The near-daily practice has clearly done its job, the same way that near-daily practice on a musical instrument does. Although Math Academy hasn’t really cured what I referred to last September as the “imp” in my brain:
The imp seems to be constantly trying to get me to make mistakes. I describe it that way because that’s what it feels like. I can be thinking (and hearing) the correct next step in solving a problem in my head, but when my hand actually writes it down, it often seems that the imp has short-circuited the messages my brain has sent to my hand, and I’ve written down something wrong.
I think the “imp” must be a pretty fundamental part of my neurology that I can only work around, not avoid completely. I wrote:
I can work around the imp somewhat, by slowly and carefully re-reading each step in my calculation and correcting any errors that I find that the imp has caused.
I’m still doing that, and it’s become a pretty solid habit by now, although if I get impatient and don’t do it, I will still get an answer wrong. It still feels like part of my brain is just waiting for an opportunity to trip me up.
By the time I got to the end of Foundations II, I had completed forty-two quizzes. That is far more evaluations than a student would get in a typical high school or college class. The sense of panic I always felt when given a timed quiz has not gone away completely, but it has lessened. My strategy of asking the system to give me a special accommodation — an extra 150% of time, so that for a ten-minute quiz, I’ll have 25 minutes — seems to have paid off. If only I had been given the opportunity to do this in high school and college, my experiences with math classes might have been significantly improved.
I’d love to be proven wrong in the future, but at the moment it doesn’t seem like I’ll ever be able to complete problems on timed quizzes at the speed the system thinks is “normal” or “typical.” I have been getting slightly faster, and now usually complete the quiz with a few minutes of my additional time left over. I try to use that time to go over any answers that I didn’t feel certain about, although that rarely helps; it seems like, in general, I can either solve the problem or I can’t. In some cases I solved it correctly with a flash of intuition, without being able to write out the steps, or by using a different method that I came up with on the fly. Sometimes my alternate method was both correct and easier than the textbook method. But when I solved a problem without using the method that I was supposed to learn, even though the system gave me credit, I still considered my answer only partially correct, because it was an indication that I had not remembered the lesson well enough. So I would still carefully go over the correct answer and write out the solution in my notebook.
A passing grade on a Math Academy quiz is, I think, about 80%. Any problems I got wrong resulted in more review assignments, and I had to complete the reviews before I could do anything else. The quiz problems ranged from pretty easy to quite difficult, and sometimes asked me to combine insights and techniques from different topics, or reason at a higher level of abstraction about things the assignments didn’t explicitly cover. If I failed a quiz, which I’d estimate I did about 20% of the time, then after I completed the assigned reviews, the system would give me the same quiz again with different questions. Math Academy has what seems like an unlimited pool of questions. Fortunately, I never found out what happened if I failed a quiz a second time. On my second tries, I usually got all the questions right.
I continue to be impressed with Math Academy, although I’ve become aware of more of its downsides, especially with the Foundations series, which combine material that would have been presented traditionally in different classes.
Because the resulting classes are so large, and take so long to complete, the time it took me to complete the class exceeded a year. Even working at it part-time, I found that I still needed an occasional break, and if I didn’t take a break, my performance would start to go downhill. I certainly considered giving up. In a semester system you’d have spring break, winter break, etc. With this system, there are no built-in breaks. It is possible to suspend an account for up to three months, but that seems like a drastic thing to do when I just need a week off. I long for a “I need a week off” button. Over the past year I’ve wound up taking maybe two full weeks off completely even without such a feature, and two or three half-weeks off when I needed a shorter break, but because the system doesn’t have any sort of support for breaks, this always left me feeling like I was doing something wrong, as well as wasting money.
Another downside may be specific to me, or perhaps specific to older people, or people experiencing some decline in their ability to memorize new information. When I was much younger, I would have been able to memorize topics, trigonometric identities, useful formulas, etc. much more easily. Now I find that even when I complete the topic, complete the review, complete a second review, and get a question about the topic correct on the quiz, following Math Academy’s “spaced repetition” of topics, which is designed to enhance memorization, I’m still completely capable of forgetting key details a few weeks later. These Foundation courses jump around — I’ll get calculus topics, algebra topics, trigonometry topics, probability and statistics topics, and linear algebra topics. This means I wind up staying away from a topic for a while, and then I have to jump back into it. When I do so, I usually find there are key things that I’ve forgotten.
Really learning all this properly, “by heart,” “down cold,” is hard at 57. I’m not sure the course design for the Foundations series is really helping me as much as it could, and in some ways I think it may be slowing me down. I am tempted to switch strategy, to for example take the standard high school classes separately, in the usual order, including AP Calculus AB and BC, but I’m not sure I really want to do that, as I’ve already covered a great deal of this material.
And so, another feature I’d like is the ability to assign myself an extra review for a topic I’ve already either covered, or tested out of initially. Sometimes I realize that even though I’ve passed the quizzes and completed the lessons and reviews, I’m not as strong in a particular topic as I would like to be. It is possible to go back and find the topic and go through it again, if it is in the course I’m currently taking, or in my case in the sequence of three courses I’ve taken. But what I’d really like is the ability to tell the system to assign me a topic to review, and treat it like a regularly assigned review. For example, I’d like to be able to do this when I get a quiz question right, but don’t solve it using the technique I was supposed to be learning.
Occasionally, a lesson will include some text that explains the intuitive rationale, or everyday meaning, behind a formula or technique. I find this very helpful. But these are unfortunately few and far between, and I sometimes find myself wishing for more of these explanations.
For example, I just completed a lesson on the dot product of vectors. The lesson explains how dot product is calculated, and then the assigned questions tested my ability to use this definition. A bit later in the lesson, it explains that if two vectors are perpendicular, the dot product of these vectors is zero. It’s easy to understand why this is, per the definition — the cosine of the difference between the angle of the vectors is a factor, and the cosine of ninety degrees is zero, so any expression that contains that factor will also be zero.
But the lesson completely fails to explain why this is true. I had to dig around into other sources to find what the dot product represents, intuitively. It serves as a measure as the extent to which vectors point in the same direction, sort of a correlation value. When I read this, it suddenly made more sense. If two vectors are pointing in opposite directions, they will have a negative dot product. If they are pointing in perpendicular directions, there is no positive or negative correlation between the directions, so it is sensible that the value will be zero.
Just recently I completed a lesson on implicit differentiation. This lesson had the same problem as the lesson on the dot product of vectors. The lesson demonstrated techniques and verified my ability to apply the technique, but completely fails to set up the technique in any kind of context. In addition, this lesson was 20 XP, which for me meant that it took over two hours to complete. That’s a big time committment. I have sent comments to the developers asking them to consider splitting very long lessons like this. There are some points where it could be easily split into two or three lessons. The lesson introduces implicit differentiation and gives a number of examples and problems. Then it asks the student to use implicit differentiation to find a slope of a tangent line, or an intercept of a tangent line. Then it moves on to asking the student to find the slope or the intercept of a normal line. The lesson could be split in half, with the second part introducing an applications of implicit differentiation, work with tangent lines or normal lines. The tangent line and normal line parts could even be broken out separately, although I would be fine with a 10 XP lesson that combines the two.
A 20 XP lesson that takes me over two hours almost guarantees that I’m going to start to experience “brain fog” towards the end without a break. That’s just the reality of my life with long COVID symptoms, and also doing these lessons at home, but not isolated in my home office, especially when it’s a hot day and I’m already sleep-deprived and I have a great deal on my plate — finding a job, managing our shrinking savings, parenting seven children, and keeping up with urgent home maintenance issues. While I got all the problems in the lesson correct, somehow between the sheer length of the lesson and the lack of context, a few days later, before repeating the topic in a review, I got a quiz question on implicit differentiation and failed it.
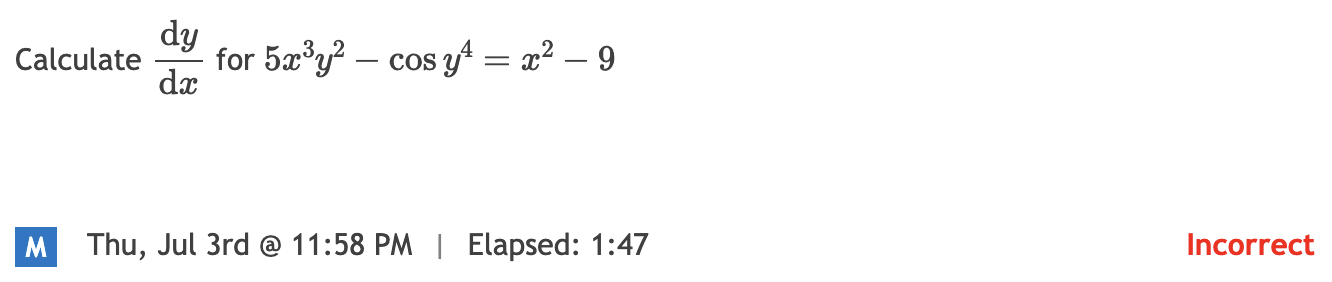
It wasn’t because I didn’t remember how to use the product rule or power rule for differentiation, or how to differentiate the cosine function; I’ve got those down. It was because I blanked on recalling the technique of implicit differentiation altogether. I think that’s because I was not clear about what it means to differentiate expressions that contain both the independent and dependent variable.
Usually the system gives me at least one review of a topic before it presents the topic on a quiz. Without that reinforcement over time, the topic hadn’t hadn’t really settled into my brain and become part of my problem-solving toolkit yet.
At these moments, I wind up feeling like Gandalf trying to find his way out of Moria:
After getting the quiz question wrong, I was assigned a review of the topic — but even after reviewing the lesson, I somehow failed that, too. I think it was mostly mental fatigue. So now I have to re-take that 20 XP lesson. That honestly feels more punitive than helpful.
Before re-taking the lesson, I pulled out my old college calculus textbook, by Swokowski, looked up that books’ explanation of implicit differentiation, and worked through the example problems. As I expected, the textook put the technique much more clearly in context. I’ll try working through the textbook exercises as well before I re-take the lesson.
I feel that this could all have been avoided if (1) the original lesson had been broken into smaller pieces, (2) the original lesson had better placed the techniques in context, and (3) the system had given me a review before testing me on this topic.
I know from the college-level textbook there’s more to understand than the Math Academy system presented to me. I have a number of other calculus textbooks in my collection that I can look at — Swokowski doesn’t always give the clearest explanations. I don’t really have a high school-level calculus textbook to compare against, but maybe I will wind up buying a used textbook on eBay, if I can pick one.
Some lessons contain a derivation of the formulas that the lesson has taught. I always get excited when I see these, although fully understanding them is described as optional, since some students won’t quite be able to follow the algebraic reasoning. Several times, this has set me up for disappointment, because several times, I have written out the derivation, line by line, and understood each step, until I came across an alegbraic step that I couldn’t follow. I felt that I almost followed it, and so this was frustrating; I felt that just a little bit of a hint at that difficult step might have made it undestandable — and also helped me learn an algebraic trick that I don’t already know. So, this was a potential “teachable moment” that just turned into frustration and disappointment. These are moments that make me keenly aware that I’m not working with a human teacher. There is a Math Academy Discord, and I have an account, and could probably jump on the Discord and perhaps have a helpful discussion with other students or the developers themselves. But this requires even more of a time committment.
Despite these things I wish were a little bit better, I still like the system enough to continue. The developers are continuing to work on the Math Academy system and on the lesson materials while I’m proceeding through the courses, so sometimes the system will give me a lesson that was added to Foundations II after I completed it. Occasionally I’ll be assigned a problem that I don’t know how to solve, and realize it’s because the system has not yet assigned me the lesson that contains that technique. But this doesn’t happen very often, and the system allows me to send feedback on problems, which I do fairly often. Not once have I come across a problem where, after studying it, I was able to convince myself that the accepted answer was incorrect, although a few months back, the system was sometimes recording an incorrect answer even when chose the correct one. That seems to have been fixed.
I’m continuing with Foundations III, which includes topics like infinite series, polar coordinates, parabolas, conic sections, Taylor polynomials, integration with partial fractions, differential equations, and other things I’ve never studied. The topics are getting more advanced, but because the whole system is organized around taking “baby steps,” they don’t seem all that daunting.
For Foundations III, I’ve decided to switch to thinner notebooks — Maruman B5 unlined notebooks:
The paper in those particular notebooks is thin, but very smooth, and the ink doesn’t show through the other side of the page. The ones I use are unlined, as I’ve experimented with lined paper, graph paper, dotted graph paper, etc., but settled on blank sheets. I’ve switched to fine-tip black pens, Staedtler 0.1mm pigment liners. I love using the mechanical pencils, especially the Pentel Orenz Nero models, which automatically advance the lead as I write, but my eyes are continuing to get worse as I age, and the black ink is quite a bit more readable than the mechanical pencil lines. This helps reduce a common type of error, in which, while solving a problem, I fail to correctly read something I just wrote.
Doing the work in pen also lets me get through my work somewhat faster, now that I’m not stopping to erase. I do occasional need to cross something out, so my Math Academy III notebooks don’t look quite as pretty as the older ones, but I can live with that. I’m trying to spend a little more time thinking and less time writing now. If I think a particular problem is going to be difficult, I’ll solve it out on scrap paper, going down any dead ends and backtracking as needed, then only copy the correct solution into my notebook, as if I was going to turn it in as a homework assignment.
The three oldest boys at home — Sam, Joshua, and Pippin — continue to make progress in their assigned Math Academy courses. Sam has passed the halfway point of Foundations II. Josh and Pippin are not taking courses in the Foundations series, which are designed for older learners for whom most of the material will be review; they’re taking “integrated” and separate courses from the high school sequence. I’m quite happy with everyone’s progress. Soon, I plan to add Benjamin to the group.
Today I’m going to share a list I’ve been working on for a long time. Between the years of 1985 and 1990, I saw many films at the College of Wooster. I’ve tried my best to recall as many of them as I can. I can’t overstate how important these films were to helping me become the person I am today. In terms of sheer number of films seen, of course I’ve seen far many more since those years than during those years. But those films hit me during my formative years — when my brain was more malleable, and when my ability to absorb visual information, and store it away, and analyze it, was arguably at its peak, at least in some ways.
Unfortunately I didn’t keep a simple journal at the time in which I recorded the names of the films as I saw them, although I do have a variety of odds-and-ends letters and other writings from that time, so as I go through those old letters and writings, I might be able to confirm some films I recall, or add some that I can’t recall.
I have been in touch with classmates and they have added a few films to this list that I don’t recall seeing myself.
Also, I have been in touch with people working at Wooster now, wondering if they might have an archive of student activity flyers that would provide a more comprehensive and organized list. So far, the responses have been negative. I thought it might be possible that the Wooster Voice, the student newspaper which was distributed in print form back then, might provide something of a record, although it does not seem like it contained a regular listing of these films.
Most of them were part of a regular series of showings in the auditorium in Mateer Hall. If I recall correctly, admission was a dollar, and two films were shown each weekend, first on Friday, and then on Saturday. Sometimes I’d watch both. Sometimes I’d watch one film on Friday, and enjoy it so much that I went back to see it on Saturday. Wooster, the city, also had a movie theater, so some of these films I may have actually watched there. As I recall, it was a fairly ordinary small theater with only two or three screens, not a giant multiplex. I also saw other films occasionally, shown elsewhere on campus, such as in a dorm lounge or classroom. For example, I saw Shoah and Aguirre, The Wrath of God in my dorm lounge. I have not included these in the list.
Between the on-campus and off-campus films, I got an amazing ad hoc education in film. Although I had enjoyed films since childhood, growing up in Erie, Pennsylvania, I didn’t see all that many. I saw big releases in theaters, and I saw films that my stepbrother Tony taped from HBO — usually horror or science fiction, such as The Fog and Battle Beyond the Stars, with an occasional drama such as Thief. But the Wooster screenings broadened my understanding of the world of film enormously.
Here is the list; it is actually several lists. Please understand that I’m aware it likely contains many omissions, and likely contains some films that weren’t actually screened at the College of Wooster during that time. The years given are the years the films were released, not the years they might have been screened. I have added a few words to summarize my feelings about the films.
I wish I had seen these at Wooster, but ultimately, I did sometimes have to actually skip films to do class work!
There’s one film that I recall, vaguely, but have not been able to find. I don’t recall the title, or the director, or the year. I recall that it was set in post-war Germany, perhaps in the 1960s, and was a German film, featuring two young women who lived together and may have been a couple; they were involved in some sort of violent resistance movement. That is sadly just about all I can recall, and some of those details may be wrong. I think I’d remember it if I saw it again, or even saw a trailer for it. I’ve wasted a lot of time trying to figure out what film it might be, and I’ve gotten nowhere.
Does this ring a bell for anyone?